최대 유량(Maximum Flow) 문제

최대 유량(Maximum Flow) 문제란?

최대 유량 문제는 주어진 방향성 그래프(네트워크)에서, 시작점(Source)에서 도착점(Sink)까지 보낼 수 있는 물질(데이터, 자원 등)의 최대 양을 구하는 문제입니다.

각 간선은 용량(Capacity) 이라는 한계를 가지며, 실제로 흐르는 양을 유량(Flow) 이라고 합니다.

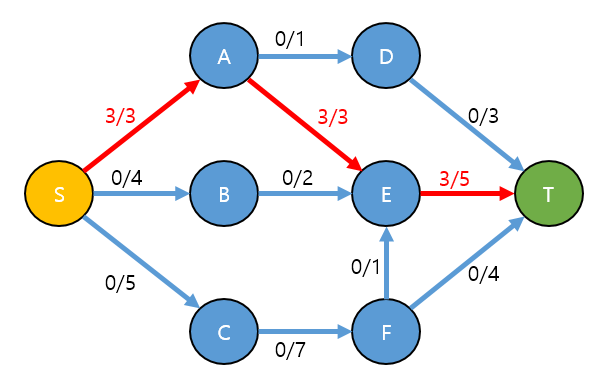
간선: 유량 / 용량

용량 제한: 각 간선의 유량은 용량을 초과할 수 없습니다.
( $f (u, v) \leq c (u, v)$ )
유량의 대칭성: u에서 v로 흐르는 유량은 v에서 u로 흐르는 음의 유량과 같습니다.
( $f (u, v) = - f (v, u)$ )
유량 보존: 시작점과 도착점을 제외한 모든 정점은 들어오는 유량과 나가는 유량의 합이 같습니다.
( $\sum_{v \in V} f (u, v) = 0$ )

잔여 용량(Residual Capacity): 특정 간선으로 더 보낼 수 있는 유량의 양입니다. ( $r (u, v) = c (u, v) - f (u, v)$ )
증가 경로(Augmenting Path): 잔여 용량이 0보다 큰 간선들로만 이루어진, 시작점에서 도착점까지의 경로입니다.

포드-풀커슨(Ford-Fulkerson) 방법은 더 이상 증가 경로가 없을 때까지 계속해서 유량을 흘려보내는 방식입니다. 이를 통해 최대 유량 문제를 해결할 수 있습니다.

모든 유량을 0으로 초기화합니다.
증가 경로를 찾습니다.
경로에 있는 간선들의 잔여 용량 중 최솟값을 찾아 그만큼의 유량을 흘려보냅니다.
유량이 흐른 간선에는 유량을 더하고, 반대 방향(역간선)에는 유량을 빼서 유량을 상쇄시킵니다. (이 과정이 잘못된 경로 선택을 되돌리는 역할을 합니다.)
증가 경로가 없을 때까지 2-4번 과정을 반복합니다.